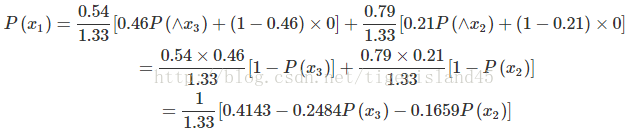来源:。
| 试题编号: | 201612-1 |
| 试题名称: | 中间数 |
| 时间限制: | 1.0s |
| 内存限制: | 256.0MB |
| 问题描述: | 问题描述 在一个整数序列a 1, a 2, …, a n中,如果存在某个数,大于它的整数数量等于小于它的整数数量,则称其为中间数。在一个序列中,可能存在多个下标不相同的中间数,这些中间数的值是相同的。 给定一个整数序列,请找出这个整数序列的中间数的值。 输入格式 输入的第一行包含了一个整数n,表示整数序列中数的个数。 第二行包含n个正整数,依次表示a 1, a 2, …, a n。 输出格式 如果约定序列的中间数存在,则输出中间数的值,否则输出-1表示不存在中间数。 样例输入 6 2 6 5 6 3 5 样例输出 5 样例说明 比5小的数有2个,比5大的数也有2个。 样例输入 4 3 4 6 7 样例输出 -1 样例说明 在序列中的4个数都不满足中间数的定义。 样例输入 5 3 4 6 6 7 样例输出 -1 样例说明 在序列中的5个数都不满足中间数的定义。 评测用例规模与约定 对于所有评测用例,1 ≤ n ≤ 1000,1 ≤ a i ≤ 1000。 |
| 试题编号: | 201612-2 |
| 试题名称: | 工资计算 |
| 时间限制: | 1.0s |
| 内存限制: | 256.0MB |
| 问题描述: | 问题描述 小明的公司每个月给小明发工资,而小明拿到的工资为交完个人所得税之后的工资。假设他一个月的税前工资(扣除五险一金后、未扣税前的工资)为S元,则他应交的个人所得税按如下公式计算: 1) 个人所得税起征点为3500元,若S不超过3500,则不交税,3500元以上的部分才计算个人所得税,令A=S-3500元; 2) A中不超过1500元的部分,税率3%; 3) A中超过1500元未超过4500元的部分,税率10%; 4) A中超过4500元未超过9000元的部分,税率20%; 5) A中超过9000元未超过35000元的部分,税率25%; 6) A中超过35000元未超过55000元的部分,税率30%; 7) A中超过55000元未超过80000元的部分,税率35%; 8) A中超过80000元的部分,税率45%; 例如,如果小明的税前工资为10000元,则A=10000-3500=6500元,其中不超过1500元部分应缴税1500×3%=45元,超过1500元不超过4500元部分应缴税(4500-1500)×10%=300元,超过4500元部分应缴税(6500-4500)×20%=400元。总共缴税745元,税后所得为9255元。 已知小明这个月税后所得为T元,请问他的税前工资S是多少元。 输入格式 输入的第一行包含一个整数T,表示小明的税后所得。所有评测数据保证小明的税前工资为一个整百的数。 输出格式 输出一个整数S,表示小明的税前工资。 样例输入 9255 样例输出 10000 评测用例规模与约定 对于所有评测用例,1 ≤ T ≤ 100000。 |
| 试题编号: | 201612-3 |
| 试题名称: | 权限查询 |
| 时间限制: | 1.0s |
| 内存限制: | 256.0MB |
| 问题描述: | 问题描述 授权 (authorization) 是各类业务系统不可缺少的组成部分,系统用户通过授权机制获得系统中各个模块的操作权限。 本题中的授权机制是这样设计的:每位用户具有若干角色,每种角色具有若干权限。例如,用户 david 具有 manager 角色,manager 角色有 crm:2 权限,则用户 david 具有 crm:2 权限,也就是 crm 类权限的第 2 等级的权限。 具体地,用户名和角色名称都是由小写字母组成的字符串,长度不超过 32。权限分为分等级权限和不分等级权限两大类。分等级权限由权限类名和权限等级构成,中间用冒号“:”分隔。其中权限类名也是由小写字母组成的字符串,长度不超过 32。权限等级是一位数字,从 0 到 9,数字越大表示权限等级越高。系统规定如果用户具有某类某一等级的权限,那么他也将自动具有该类更低等级的权限。例如在上面的例子中,除 crm:2 外,用户 david 也具有 crm:1 和 crm:0 权限。不分等级权限在描述权限时只有权限类名,没有权限等级(也没有用于分隔的冒号)。 给出系统中用户、角色和权限的描述信息,你的程序需要回答多个关于用户和权限的查询。查询可分为以下几类: * 不分等级权限的查询:如果权限本身是不分等级的,则查询时不指定等级,返回是否具有该权限; * 分等级权限的带等级查询:如果权限本身分等级,查询也带等级,则返回是否具有该类的该等级权限; * 分等级权限的不带等级查询:如果权限本身分等级,查询不带等级,则返回具有该类权限的等级;如果不具有该类的任何等级权限,则返回“否”。 输入格式 输入第一行是一个正整数 p,表示不同的权限类别的数量。紧接着的 p 行被称为 P 段,每行一个字符串,描述各个权限。对于分等级权限,格式为 <category>:<level>,其中 <category> 是权限类名,<level> 是该类权限的最高等级。对于不分等级权限,字符串只包含权限类名。 接下来一行是一个正整数 r,表示不同的角色数量。紧接着的 r 行被称为 R 段,每行描述一种角色,格式为 <role> <s> <privilege 1> <privilege 2> ... <privilege s> 其中 <role> 是角色名称,<s> 表示该角色具有多少种权限。后面 <s> 个字符串描述该角色具有的权限,格式同 P 段。 接下来一行是一个正整数 u,表示用户数量。紧接着的 u 行被称为 U 段,每行描述一个用户,格式为 <user> <t> <role 1> <role 2> ... <role t> 其中 <user> 是用户名,<t> 表示该用户具有多少种角色。后面 <t> 个字符串描述该用户具有的角色。 接下来一行是一个正整数 q,表示权限查询的数量。紧接着的 q 行被称为 Q 段,每行描述一个授权查询,格式为 <user> <privilege>,表示查询用户 <user> 是否具有 <privilege> 权限。如果查询的权限是分等级权限,则查询中的 <privilege> 可指定等级,表示查询该用户是否具有该等级的权限;也可以不指定等级,表示查询该用户具有该权限的等级。对于不分等级权限,只能查询该用户是否具有该权限,查询中不能指定等级。 输出格式 输出共 q 行,每行为 false、true,或者一个数字。false 表示相应的用户不具有相应的权限,true 表示相应的用户具有相应的权限。对于分等级权限的不带等级查询,如果具有权限,则结果是一个数字,表示该用户具有该权限的(最高)等级。如果用户不存在,或者查询的权限没有定义,则应该返回 false。 样例输入 3 crm:2 git:3 game 4 hr 1 crm:2 it 3 crm:1 git:1 game dev 2 git:3 game qa 1 git:2 3 alice 1 hr bob 2 it qa charlie 1 dev 9 alice game alice crm:2 alice git:0 bob git bob poweroff charlie game charlie crm charlie git:3 malice game 样例输出 false true false 2 false true false true false 样例说明 样例输入描述的场景中,各个用户实际的权限如下: * 用户 alice 具有 crm:2 权限 * 用户 bob 具有 crm:1、git:2 和 game 权限 * 用户 charlie 具有 git:3 和 game 权限 * 用户 malice 未描述,因此不具有任何权限 评测用例规模与约定 评测用例规模: * 1 ≤ p, r, u ≤ 100 * 1 ≤ q ≤ 10 000 * 每个用户具有的角色数不超过 10,每种角色具有的权限种类不超过 10 约定: * 输入保证合法性,包括: 1) 角色对应的权限列表(R 段)中的权限都是之前(P 段)出现过的,权限可以重复出现,如果带等级的权限重复出现,以等级最高的为准 2) 用户对应的角色列表(U 段)中的角色都是之前(R 段)出现过的,如果多个角色都具有某一分等级权限,以等级最高的为准 3) 查询(Q 段)中的用户名和权限类名不保证在之前(U 段和 P 段)出现过 * 前 20% 的评测用例只有一种角色 * 前 50% 的评测用例权限都是不分等级的,查询也都不带等级 |
试题编号: 201612-4
试题名称: 压缩编码 时间限制: 3.0s 内存限制: 256.0MB 问题描述: 问题描述 给定一段文字,已知单词a1, a2, …, an出现的频率分别t1, t2, …, tn。可以用01串给这些单词编码,即将每个单词与一个01串对应,使得任何一个单词的编码(对应的01串)不是另一个单词编码的前缀,这种编码称为前缀码。 使用前缀码编码一段文字是指将这段文字中的每个单词依次对应到其编码。一段文字经过前缀编码后的长度为: L=a1的编码长度×t1+a2的编码长度×t2+…+ an的编码长度×tn。 定义一个前缀编码为字典序编码,指对于1 ≤ i < n,ai的编码(对应的01串)的字典序在ai+1编码之前,即a1, a2, …, an的编码是按字典序升序排列的。 例如,文字E A E C D E B C C E C B D B E中, 5个单词A、B、C、D、E出现的频率分别为1, 3, 4, 2, 5,则一种可行的编码方案是A:000, B:001, C:01, D:10, E:11,对应的编码后的01串为1100011011011001010111010011000111,对应的长度L为3×1+3×3+2×4+2×2+2×5=34。 在这个例子中,如果使用哈夫曼(Huffman)编码,对应的编码方案是A:000, B:01, C:10, D:001, E:11,虽然最终文字编码后的总长度只有33,但是这个编码不满足字典序编码的性质,比如C的编码的字典序不在D的编码之前。 在这个例子中,有些人可能会想的另一个字典序编码是A:000, B:001, C:010, D:011, E:1,编码后的文字长度为35。 请找出一个字典序编码,使得文字经过编码后的长度L最小。在输出时,你只需要输出最小的长度L,而不需要输出具体的方案。在上面的例子中,最小的长度L为34。 输入格式 输入的第一行包含一个整数n,表示单词的数量。 第二行包含n个整数,用空格分隔,分别表示a1, a2, …, an出现的频率,即t1, t2, …, tn。请注意a1, a2, …, an具体是什么单词并不影响本题的解,所以没有输入a1, a2, …, an。 输出格式 输出一个整数,表示文字经过编码后的长度L的最小值。 样例输入 5 1 3 4 2 5 样例输出 34 样例说明 这个样例就是问题描述中的例子。如果你得到了35,说明你算得有问题,请自行检查自己的算法而不要怀疑是样例输出写错了。 评测用例规模与约定 对于30%的评测用例,1 ≤ n ≤ 10,1 ≤ ti ≤ 20; 对于60%的评测用例,1 ≤ n ≤ 100,1 ≤ ti ≤ 100; 对于100%的评测用例,1 ≤ n ≤ 1000,1 ≤ ti ≤ 10000。 试题编号: 201612-5 试题名称: 卡牌游戏 时间限制: 3.0s 内存限制: 256.0MB 问题描述: 问题描述 小Q和小M是游戏数值策划师,他们最近在测试自己新设计的卡牌对战游戏。游戏总共有 n 张卡牌,用 1 到 n 的正整数编号。最开始小Q和小M各会拥有其中的一部分。 每一局游戏,小Q和小M都需要从自己拥有的卡牌中选出一张进行对战,获胜的一方会获得双方选出的两张卡牌。游戏会一直进行下去,直到其中一个人获得了所有的卡牌,此时获得所有卡牌的一方赢得了最终的胜利。 对于一对特定的卡牌 i 和 j,i 战胜 j 的概率为 Pi, j。此概率与其他事件独立,只与选出的这两张卡牌有关系;每次对战一定会决出胜负,因此有 Pi,j + Pj,i = 1。 小Q和小M都没有好好学习博弈论,已经忘了混合决策那套理论。经过商量,他们采取了同一套看起来合理的选牌方式: 1. 对于自己的卡牌 i,计算出这张卡牌能赢得对方每张卡牌的概率之和 Si=∑j是对方的卡牌Pi, j ; 2. 令自己选出卡牌i的概率正比于Si,即选出i的概率为 Si/∑k是自己的卡牌Sk。 小M想知道,对于给出的 m 种初始状态,他最终获胜的概率是多少。 输入格式 从标准输入读入数据。 输入的第一行包含两个正整数 n, m 表示卡牌的数量和初始状态的数量。 接下来 n-1 行。其中的第 i 行(1 ≤ i < n)包含 n - i 个恰好含有 2 位小数的浮点数;该行的第 j 个(1 ≤ j ≤ n - i)数表示 Pi, i+j。 保证上述每个 Pi,j 均是直接调用伪随机数生成函数生成一个 [10, 90] 上的整数,然后除以 100 得到;即可以认为每个数都是从 [0.10, 0.90] 上的所有 2 位小数中,独立等概率取得的。 接下来 m 行,每行包含 n 个 0 或 1 的整数,描述一个初始状态。这 n 个数中的第 i 个如果是 1 表示第 i 张牌最初在小M手中,否则表示这张牌在小Q手中。 保证询问两两不同。 输出格式 输出到标准输出。 输出 m 行,每行输出一个小数部分长度恰好为5的浮点数,表示小M的每种初始状况最终获胜的概率四舍五入后的结果。 你答案中的每个数必须和参考答案完全一样才能获得相应测试点的分数。 保证参考答案与真实答案的差值不超过 4 × 10-6。 样例输入 3 4 0.46 0.21 0.86 0 0 0 1 1 0 0 0 1 1 1 1 样例输出 0.00000 0.83488 0.16512 1.00000 样例说明| 局面编号 | 小M的牌 | 小Q的牌 | S1 | S2 | S3 | 小M的 Si 之和 | 小Q的 Si 之和 |
| x1 | 1 | 2,3 | 0.67 | 0.54 | 0.79 | 0.67 | 1.33 |
| x2 | 2 | 1,3 | 0.46 | 1.40 | 0.14 | 1.40 | 0.60 |
| x3 | 3 | 1,2 | 0.21 | 0.86 | 0.93 | 0.93 | 1.07 |
我们设 P (x) 为当前局面为 x,最终小M获胜的概率,例如 P (x1) 表示小M手里的牌为 1 最终获胜的概率。 定义事件 ^x 为将局面 x 中双方手里的牌互换的局面,根据对称性易得 P( ^x)=1 - P (x)。 对于全部牌都在小M手里的情况,小M已经赢得了胜利,此种情况下小M获胜概率为 1;相反,牌全部在小Q手里的话,小M获胜概率为 0。 对于局面 x1:小M由于只有一张牌 1,因此他必须出这张牌;小Q根据之前的选牌策略,他有 0.54/1.33 的概率出 2,有 0.79/1.33 的概率出 3。若小Q出 2:则小M有 0.46 的概率会赢得这张牌,从而进入局面 ^x3;有 1-0.46 的概率会输掉手中最后一张 1。若小Q出 3:则小M有 0.21 的概率会赢得这张牌,从而进入局面 ^x2;有 1-0.21 的概率会输掉最后一张 1。因此,可以得出